Avant d’entrer dans le vif du sujet, il est nécessaire de mettre au point la définition d’une orbite , de l’espace et de mieux comprendre les lois de la physiques qui sont à la source de ce phénomène.
A)Mais qu’est ce qu’ une orbite?
Avant toute chose il est important de définir ce qu’est une orbite et ce que cela implique!
La notion d’orbite est utilisée en astronomie pour désigner la trajectoire d’un corps céleste (une étoile, une planète, un satellite naturel ou artificiel) autour d’un autre corps céleste. Cette trajectoire est dite périodique c’est-à-dire qu’elle se reproduit à intervalles réguliers : la Terre fait le tour du Soleil en 365 jours. L’orbite est un phénomène observable à de nombreuses échelles au sein de notre Univers :
- La Terre est en orbite autour du Soleil.
- La lune est en orbite autour de la Terre.

L’explication ? La gravitation Universelle
Découverte par le physicien anglais Isaac Newton en 1687, la gravitation Universelle a permis de mettre en évidence que tous les objets de notre Univers s’attirent entre eux. La Terre attire le satellite tout comme le satellite attire la Terre! Sur Terre on parle de pesanteur à ne pas confondre avec L’Apesanteur

C’est en 1729 que le physicien Isaac Newton publie dans son ouvrage A Treatise of the System of the World ,une expérience de pensée que l’on appellera « Le canon de Newton ».
Dans celle-ci Newton imagine un canon situé au sommet d’une montagne et tirant des boulets avec une vitesse initiale de plus de plus importante. Le boulet décrira d’abord une trajectoire parabolique avant de retomber sur Terre, puis au fur et à mesure que sa vitesse initiale augmente, la distance qu’il parcourt se fera plus grande également.
🤔OK, mais comment ça marche exactement ?
C’est la courbure de la Terre qui va nous permettre de placer un objet en orbite, on dit que l’objet « tombe constamment sur la Terre », mais celle-ci s’en éloigne tout autant.
Newton va alors stipuler qu’il existe un premier seuil de vitesse à partir duquel la courbe décrite par le boulet épouse parfaitement la courbe de la Terre, celui-ci est alors satellisé en orbite circulaire.
Enfin il existe un deuxième seuil de vitesse, au-delà de celle-ci, le boulet échappe à la Terre et continue sa route vers l’espace. Toute vitesse comprise entre ses deux seuils permettra au boulet de décrire une orbite elliptique.
Nous avons réalisé une animation afin d’illustrer les pensées de Newton en remplaçant le canon par une personne :
Principe de la mise en orbite from Fahloul Hanane on Vimeo.
Cette vitesse initiale acquise par l’objet est la clé de la satellisation, c’est cette vitesse qui permettra aux scientifiques de placer en orbite les satellites qu’ils ont conçus leur permettant non pas de vaincre la pesanteur mais de la compenser .
L’effet centrifuge
Essayons d’apporter une explication à tout cela.
En l’absence de toute force exercée sur le satellite, celui-ci continuerait sa route dans l’espace en suivant une trajectoire rectiligne uniforme. Mais la force d’attraction exercée par la Terre va faire dévier le satellite de sa trajectoire, l’entraînant vers son centre de gravité G. Mais le satellite va venir s’opposer à ce changement : c’est le principe d’inertie.
Pour mettre un objet en orbite il faut parvenir à le propulser avec une vitesse initiale telle que celui-ci soit toujours attiré vers le centre G de la Terre, mais sa vitesse tangentielle (perpendiculaire au vecteur G qui relie le centre de la Terre au centre du satellite) crée une force d’inertie qui le pousse à poursuivre son chemin en ligne droite.

L’effet centrifuge peut donc être défini comme la résistance au changement de direction d’un objet imposé par la force centripète (« qui tend à se rapprocher du centre » en latin) est dû à l’inertie de la masse.

Sa formule est la suivante:
Elle se calcule en faisant le produit de la masse de l’objet et de son accélération centrifuge notée a
On sait donc maintenant que la capacité d’un objet à maintenir son orbite vient de l’équilibre entre sa vitesse en ligne droite (vitesse dite tangentielle à la trajectoire) et la pesanteur qui agit sur lui à chaque instant et l’attire vers le centre de la Terre.
On s’interroge à présent sur cette fameuse vitesse que l’on va chercher à calculer.
B) La vitesse de satellisation
Note: Pour les calculs de vitesse , nous supposerons que les orbites étudiées sont circulaires ,afin de simplifier les calculs. On supposera également que la vitesse du satellite est constante.
Quelle est la vitesse à imprimer à notre satellite pour lui permettre de se mettre en orbite autour de la Terre ?
Lorsque l’on lâche un objet, celui-ci retombe vers le sol, soumis à la gravité terrestre. Pour placer un objet en orbite autour de la Terre, celui-ci doit parvenir à vaincre cette force d’attraction. (voir expérience de Newton)
Seulement la Terre est ronde, elle est aussi décrite une courbe. L’objet ayant atteint une certaine vitesse, il décrira une courbe telle qu’elle épousera parfaitement la courbure de la Terre et ne touchera plus le sol . On dit que l’objet est constamment entrain de tomber . Mais, dû à sa courbure, la Terre s’en éloigne tout autant. À chaque instant l’objet est soumis à la gravité terrestre mais sa vitesse en ligne droite lui permet de résister à cette attraction : c’est la vitesse de satellisation.
Nous allons tenter de déterminer cette vitesse de satellisation en supposant que l’orbite est circulaire (nous verrons plus tard que la majorité des orbites sont elliptiques):
On modélise la situation en faisant un schéma puis on réalise un bilan des forces:
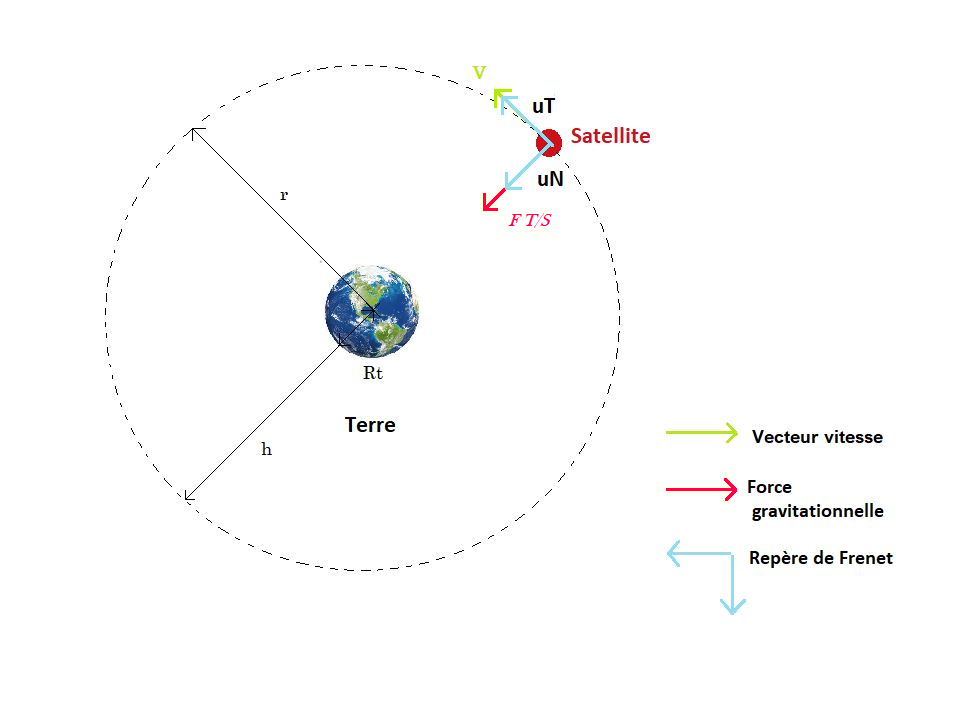
Force s’appliquant sur le satellite:
attraction gravitationnelle ayant pour sens le centre de la Terre.
Afin d’étudier le mouvement du satellite, on se place dans un référentiel géocentrique ayant pour origine le centre de la Terre et ses axes définis sur 3 étoiles lointaines , mais étant donné que notre expérience se déroule sur une période de temps assez courte, on peut le considérer comme un référentiel Galiléen.
« Un référentiel galiléen, ou inertiel, se définit comme un référentiel dans lequel le principe d’inertie est vérifié, c’est-à-dire que tout corps ponctuel libre est en mouvement de translation rectiligne uniforme, ou au repos. »
Le système étudié est le satellite, de masse m . La force s’exerçant sur lui est la gravité .
Newton énonça la loi de la gravité comme suit:
«Les astres s’attirent de façon proportionnelle au produit de leur masse et inversement proportionnelle au carré de la distance qui les sépare.»
En traduisant cela donnerait:

Avec M et m les masses respectives de la Terre et du satellite en kg r la distance qui les séparent et G la constante gravitationnelle.
Pour trouver V (vitesse) on va utiliser la deuxième loi de Newton :
« Dans un référentiel galiléen, la somme vectorielle des forces appliquées à un objet ponctuel est égale au produit de la masse de l’objet par son vecteur accélération »
http://eduscol.education.fr/orbito/orb/meca/meca12.htm
🤔 Mais qu’est ce que cela veut dire?
Dans un référentiel galiléen, la somme des vecteurs représentant les forces s’exerçant sur un corps ponctuel – c’est-à-dire qui peut être représenté par un point M associé à une masse m – est égale au produit de la masse du corps par son vecteur accélération.
Elle s’écrit :

avec m la masse du satellite et a le vecteur accélération Cette accélération est normalement constituée de deux vecteurs , un tangent et l’autre normal à la trajectoire.
L’accélération a d’un objet est formée de deux composantes : une accélération tangentielle aT et une accélération normale à la trajectoire aN. Elles s’expriment ici dans le repère de Frenet défini par 2 vecteurs unitaires uT et uN (voir image) avec pour origine le centre du satellite : c’est donc un repère en mouvement.

🤔Mais notre satellite va a une vitesse constante, il ne subit donc pas d’accélération ?
L’accélération tangentielle est calculée en faisant la dérivée de la vitesse , ici notre satellite possède une vitesse constante, cette accélération est nulle. Cependant si on s’intéresse à la direction du vecteur vitesse, on se rend compte qu’elle n’est pas la même à deux instants t différents. Il y a donc bien une variation du vecteur vitesse. Il semble se rapprocher de la trajectoire. L’objet subit une accélération normale ou centripète
Cette accélération n’agit que sur la composante verticale de la vitesse, c’est à dire le vecteur uN.
On a donc:

D’après la deuxième loi de Newton:

On aurait alors :

<=>

<=>

<=> car m # 0
On obtient alors :

Application numérique:
On dispose des données suivantes:
- La constante gravitationnelle G : 6.674*10^(-11)
- La masse de la Terre M : 5.972.10^24 kg
- Le rayon de la Terre r : 6371 km
- D la hauteur de l’orbite (distance entre surface de la Terre et le satellite)
On calcule V au sol soit D = 0



Cette valeur reste théorique . En effet il est pratiquement impossible de placer un objet en orbite à moins de 200km d’altitude à cause des frottements de l’air.
Voici une courbe tracée grâce au logiciel Excel représentant la valeur de la vitesse d’un satellite pour des altitudes D allant de 200 à 40000 km d’altitude:

On constate une diminution de la vitesse de satellisation: d’après la loi de Newton , plus deux objets sont éloignés l’un de l’autre et moins la force de pesanteur se fait ressentir!
On sait donc que pour mettre un satellite en orbite, il faut lui fournir une vitesse qui sera de moins en moins grande à mesure que le satellite s’éloigne. À l’inverse plus il sera mis en orbite proche de la Terre, plus il devra aller vite pour compenser la gravité.
C)Les différents types d’orbite
Nous avons donc vu comment le phénomène de mise en orbite était rendu possible grâce à l’action simultanée des forces gravitationnelles et de la vitesse sur le satellite. Un satellite peut-être mit sur un nombre infini d’orbites différentes présentant chacune des caractéristiques précises adaptées ou pas à la mission du satellite.
On peut distinguer principalement 3 types d’orbites terrestres: les orbites basses, les orbites moyennes et les orbites hautes:

- Les orbites basses sont principalement utilisées par les satellites scientifiques comme par exemple le télescope Hubble.
- En orbite moyenne on retrouve des satellites de navigation ainsi que des satellite GPS.
- Enfin en orbite haute ce sont des satellites météorologiques et des satellites de télécommunication qui orbitent.
Nous avons vu précédemment que c’est l’altitude de l’orbite qui détermine la vitesse à laquelle le satellite se déplace autour de la Terre. En jouant sur ce paramètre , on peut avoir une influence sur la période de révolution du satellite ou encore la forme de son orbite.

La période de révolution notée T d’un satellite désigne le temps qu’il lui faut pour faire une fois un tour complet de la Terre.
L’excentricité notée e exprime l’écart entre la forme de l’orbite et celle d’une orbite parfaitement circulaire.
Les vitesses calculées précédemment sont celles d’un satellite en orbite circulaire. À une altitude de 10 000 km par exemple, un satellite doit avoir une vitesse de 5 km /s. Un satellite géostationnaire situé à 36 000 km de la Terre lui ne nécessite « qu’une vitesse de 3,04 km /s
Si maintenant pour une même altitude le satellite possède une vitesse supérieure à celle-ci, alors son orbite ne sera plus circulaire mais elliptique.
Autres paramètres orbitaux:
- L’inclinaison orbitale notée i désigne l’angle entre le plan de l’équateur terrestre et le plan de l’orbite
- La longitude du noeud ascendant notée Ω correspond au point d’intersection entre le plan de l’équateur et l’orbite et marque le passage de l’hémisphère sud vers l’hémisphère nord.
Pour toute altitude cependant, une vitesse excédant les 11,2 km/s ne permettra plus au satellite de rester en orbite, sa trajectoire décrira donc une hyperbole ou une parabole et il s’éloignera définitivement de la Terre: c’est la vitesse de libération
Voyons ensemble les principaux types d’orbites utilisées et leurs principales caractéristiques: