Nous avons vu précédemment comment un satellite pouvait être mis en orbite depuis la Terre, cependant dans certains cas il peut être nécessaire de passer par ce qu’on appelle une orbite de transfert ou temporaire depuis laquelle le satellite ira se placer sur son orbite définitive grâce à la poussée de ses propres moteurs.

Jusqu’à présent nous avons supposé que les orbites étaient circulaires et que la vitesse du satellite était constante. Nous allons voir que ce n’est pas toujours le cas en pratique.

A)Les lois de Kepler

Nous avons dans un premier temps fait des recherches sur les lois de Kepler qui régissent les mouvements des planètes autour du Soleil. Ces lois peuvent également s’appliquer à des satellites en orbite autour de la Terre.

Le logiciel Planet orbit simulator nous a permis de nous familiariser avec ces lois et de mieux les comprendre.

La première loi de Kepler

On ne se servira pas de cette loi mais il est toujours bon de la connaitre 😉

La trajectoire des planètes autour du Soleil est une ellipse, dont le Soleil est un des deux foyers:

Pour rappel, une ellipse en mathématiques est un cercle dont l’excentricité est comprise entre 0 et 1, elle possède deux foyers nommés F et F’.

Deuxième loi de Kepler: La loi des aires

Cette fois-ci les choses se corsent un peu , la seconde loi de Kepler nous dit que le rayon vecteur reliant un des deux foyers à la planète balaie des aires égales en des intervalles de temps égaux.

Pour illustrer ces propos nous retournons sur notre logiciel et utilisons l’option « sweeping » qui signifie « balayage » pour un intervalle de temps Δt. On augmente volontairement l’excentricité de l’orbite afin que l’effet soit observable :

D’après la deuxième loi de Kepler, ces deux aires sont de même valeur, l’explication est que la vitesse de la planète n’est pas la même suivant l’endroit où elle se trouve sur son orbite.

Un point très important: plus la distance entre le foyer de l’orbite et l’objet en orbite est grande, moins la force d’attraction se fait ressentir.

Le point le plus éloigné du Soleil porte le nom d’aphélie , le point le plus proche celui de périhélie. Pour un satellite en orbite autour de la Terre on parlera d’apogée et de périgée

 Troisième loi de Kepler ou « Loi des périodes »

Cette loi permet de savoir la distance à laquelle un corps se trouve par rapport au Soleil si on connaît sa période de révolution. D’après l’énoncé de cette loi, le carré de la période de révolution est proportionnel au cube du demi-grand axe (ou rayon) de l’orbite.

Cette loi s’applique également aux satellites artificiels comme en témoigne ce graphique. Il a été tracé en prenant comme valeur les périodes de révolutions et le rayon de l’orbite de 4 satellites: GALILEO METESAT GPS et GLONASS.

B)Le transfert d’Hohmann

Maintenant que l’on sait tout cela, on peut passer à la partie mise en pratique. Notre objectif ici va être de déterminer la vitesse nécessaire à fournir à un satellite pour lui faire changer d’orbite.

Nous avons réalisé en classe une analogie du phénomène avec celui d’un électron qui changeait de couche:

Le lanceur Ariane 5 est utilisé principalement pour envoyer des satellites en orbite géostationnaire à 36 000 km au-dessus de nos têtes. Atteindre une telle altitude ne pose en théorie pas de problème particulier. Seulement, en pratique, on a recours à ce qu’on appelle un transfert d’orbite.

L’orbite cible étant beaucoup trop éloignée, la mise en orbite se fait en plusieurs étapes:

1. L’injection par le lanceur sur une première orbite circulaire d’altitude h1 = 250 km avec une vitesse v1
2. Le satellite utilise ses moteurs pour se placer sur une orbite de transfert elliptique dont le périgée se situe sur l’orbite initiale et dont l’apogée se trouve sur l’orbite finale d’altitude h2= 35 943 km.
3. Une fois arrivé à l’apogée de l’orbite de transfert, on fournit au satellite un dernier supplément de vitesse v » qui lui permettra d’atteindre son orbite circulaire définitive d’altitude h2= 35943 km

Nous avons réalisé un schéma illustrant ce processus :

😮Pourquoi fait t-on cela?

Tout est une question d’énergie! Comme nous le verrons juste après, l’énergie mécanique nécessaire à fournir au satellite est reliée au rayon de l’orbite, d’où l’utilisation d’une orbite elliptique. Une fois à son apogée, il ne restera plus qu’à lui donner un soupçon de vitesse et le tour est joué!

Note: le lanceur Ariane 5 est si puissant qu’il peut envoyer directement le satellite en orbite elliptique sans passer par l’étape 1. Nous prendrons tout de même compte de cette étape dans notre raisonnement.

Transfert d’orbite: Mode d’emploi

Étape 1: Déterminer les vitesse v1 et v2

Grâce à la formule que nous avons utilisée pour calculer la vitesse de satellisation (voir Vitesse de satellisation), on détermine les vitesses v1 et v2 aux altitudes respectives de 250 km et 35943 km:

Nous déterminons l’énergie mécanique du satellite sur son orbite 1 puis sur son orbite de transfert. L’énergie mécanique est la somme de l’énergie cinétique Ec et de l’énergie potentielle Ep :

On appelle E1 l’énergie mécanique du satellite sur son orbite 1 et E2 celle sur son orbite de transfert.

Ici le rayon de l’orbite est remplacé par le demi-grand axe de l’ellipse

La vitesse v’ à fournir au satellite pour passer de l’orbite 1 à l’orbite de transfert dépend de l’énergie mécanique nécessaire, soit E2-E1= 3.29.10^10 J

La variation d’énergie mécanique ne dépend que de l’énergie cinétique, la distance à la terre (périgée-centre de la Terre) étant la même sur les 2 orbites.

On obtient donc:

De la même manière:

C) Limites et évolutions

En réalité, tout n’est pas aussi simple que ça en à l’air…

La latitude de la base peut également agir sur le type d’orbite qui pourra être atteint par le lanceur et notamment son inclinaison c’est-à-dire l’angle entre le plan de l’orbite et celui de l’équateur en degrés. Il est nécessaire que le point de lancement soit situé dans l’orbite cible, autrement elle ne peut être atteinte. Lors du lancement la direction que prendra le lanceur porte le nom d’azimut, il s’agit en quelque sorte de l’angle entre le Nord et la direction du lanceur . (Est=90°) (image)

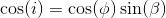
En pratique il existe une marge entre l’orbite cible/définitive et l’orbite réellement atteinte à l’issue du lancement. Des facteurs comme les conditions environnementales peuvent influencer la trajectoire de la fusée. Les calculs effectués précédemment sont donc simplement théoriques. Le lanceur Ariane 5 est un des plus précis sur le marché, avec un écart pour une orbite géostationnaire de 1,3 km au périgée et de 80 km à l’apogée.

Une fois sur son orbite de travail le satellite va subir de nombreux phénomènes naturels qui vont venir perturber sa trajectoire.

1-La Terre n’est pas tout à fait ronde

Le premier d’entre eux est l’aplatissement de la Terre aux pôles et à son renflement à l’équateur : la Terre n’est pas une sphère parfaite. Ce phénomène entraîne une déformation de l’orbite.

2- Le champ de gravité peut varier

La pesanteur sur Terre n’est pas la même selon l’endroit où on se situe, pour la raison évoquée précédemment mais aussi

Ici , une animation proposée par le site de la National Aeronautics and Space Administration représentant la variation de la valeur de la gravité par rapport à la valeur « standard » déterminée en considérant la Terre comme étant une sphère parfaitement lisse.
Les zones en bleue possèdent une valeur inférieure à celle estimée, les zones en rouge une valeur supérieure.
Conséquences : la variation de la pesanteur aura des conséquences sur la stabilité de l’orbite du satellite

3- L’atmosphère ralentit (toujours) le satellite

On imagine souvent l’atmosphère comme une enveloppe de gaz qui recouvrirait notre planète et qui marquerait la limite entre le ciel et l’espace.

Dans les faits, il n’y a pas de limite entre l’atmosphère terrestre et l’espace. Plus l’altitude augmente, moins l’atmosphère est dense. Ainsi elle peut s’étendre jusqu’à près de 50 000 km d’altitude! La force de traînée engendrée par les frottements de l’air agit sur la trajectoire du satellite qui voit son altitude diminuer au cours du temps.

Une limite a cependant été décrété par le physicien Theodore von Karman et se situe à 100 km d’altitude: c’est la ligne de Karman ( pour plus d’informations voir: https://fr.wikipedia.org/wiki/Ligne_de_K%C3%A1rm%C3%A1n )

Il en résulte que la durée de vie moyenne d’un satellite diminue lorsque celui-ci se rapproche de la Terre. Ainsi pour une orbite circulaire à 200 km d’altitude, le satellite finit par rentrer dans les couches denses de l’atmosphère en l’espace de quelques jours seulement, tandis qu’un satellite en orbite géostationnaire lui a une durée de vie d’un million d’années.

Les évolutions

Le monde de l’aérospatial est en constante évolution afin de répondre aux besoins des scientifiques. L’objectif est de parvenir à envoyer des satellites de moins en moins lourds afin de pouvoir emporter plus d’outils à bord, mais aussi de diminuer le coût d’un lancement qui peut s’avérer cher.

• Le système de propulsion électrique pourrait remplacer les moteurs actuels alimentés en ergols qui prennent plus d’espace. L’entreprise Airbus Defence and Space est ainsi parvenue a économiser jusqu’à 40% du poids de lancement. Le seul inconvénient est la durée de transfert en orbite géostationnaire passant d’une semaine à 6 mois.
• L’utilisation de lanceurs réutilisables comme Falcon 9 (Space X) pourrait permettre de réaliser jusqu’à 30 % d’économies sur le prix d’un lancement.

• 

• 

Un satellite possède une durée de vie estimée entre 15 et 20 ans, durée au delà de laquelle il n’est plus opérationnel, généralement quand il n’a plus suffisamment d’ergols.
Afin de laisser la place à de nouveaux satellites, celui ci doit être très rapidement enlevé de son orbite, plusieurs cas sont rencontrés:

1. Soit le satellite se trouve sur une orbite basse, au quel cas il est placé sur une orbite assurant sa destruction complète dans l’atmosphère d’ici 25 ans. C’est le cas du satellite METOP-7 le 3 avril 2017.
2. S’il se situe sur une orbite géostationnaire, le satellite est redirigé vers une orbite dite « cimetière » située 200 km au dessus.

Cependant il peut arriver que le satellite tombe en panne prématurément ou qui n’ont plus suffisamment d’ergols pour réaliser les manœuvres nécessaires: ils constituent alors un débris gênant.

S’il est possible de savoir combien de lancement orbitaux ont lieu, il est assez difficile de pouvoir dire avec précision le nombre de satellites qui orbitent au-dessus de nos têtes, notamment en raison des lancements multiples. De plus certains lancements (satellites espions) sont souvent gardés secrets.

De même, le nombre de débris spatiaux reste approximatif. Ces débris sont issus d’anciennes collisions entre satellite, pouvant occasionner ce qu’on appelle le Syndrome de Kessler, un scénario dans lequel le nombre de débris spatiaux serait si grand qu’il rendrait impossible l’envoi de satellite artificiels.

•